
How to Calculate Standard Deviation in Excel
Standard deviation is a statistical term to show us the range between average and the actual data. It allows us to understand the variability and consistency of the data. The higher standard deviation means larger dispensation while lower standard deviation means the data is consistent.
When working with a numeric data set, you usually want to know what the standard element of the set is. You can try finding the mean or the median but the middle of the set does not give reliable information about the set.
Mean: The sum of all the individuals divided by the number of individuals.
Median: The individual that stands in the middle of sorted from low to high.
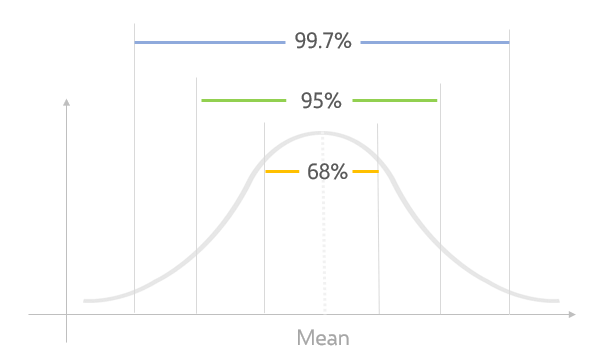
The standard deviation shows how consistent are the individuals are in this data set. Therefore it is commonly used and very important.
Recommended Reading: How to Normalize Data in Excel?
How To Calculate Standard Deviation Mathematically
Let us show you how to calculate the Standard date by giving a very simple example. Let’s say you have a set of numeric data: 4, 6, 8, 12, 15.
First, you should find the mean by you add all the numbers and divide them to the number of individuals in the data set. In this case, it is 45/5. So the mean is 9.

Then, subtract all the numbers from the mean and square them so all the results will be positive instead of negative. It will be added up all these squared numbers to each other and divide them to one less of the number of individuals in our data set (which is 4 in this example).
Just take the square root of the equation and there you are! You calculated the standard deviation. It is 4.
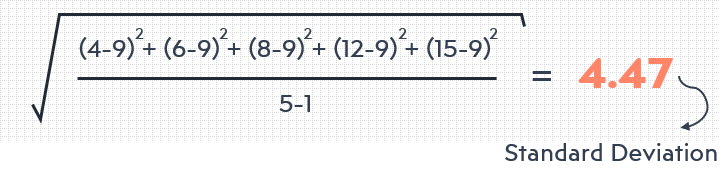
Why Standard Deviation Is an Important Statistic?
The standard deviation has vital importance in matters like finances. You can’t calculate the risk by considering the only average. It might give you a superficial opinion of the data but it is not healthy or informed enough.
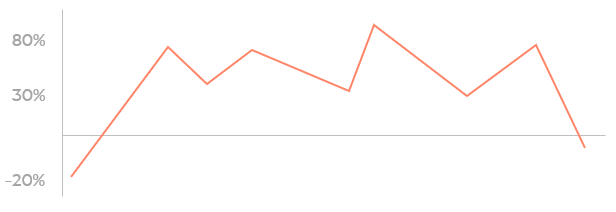
Let’s say you are about to invest some money on a company and they tell you investors gain 30% back at the end of the year. What this data will tell you is that the gain can differ from -20% to 80%.
You applied for a job and you are told the average salary of a company’s personnel is 20.000 dollars. This might seem amazing but what if the salaries variated from 1.000 dollars to 19.000 dollars?
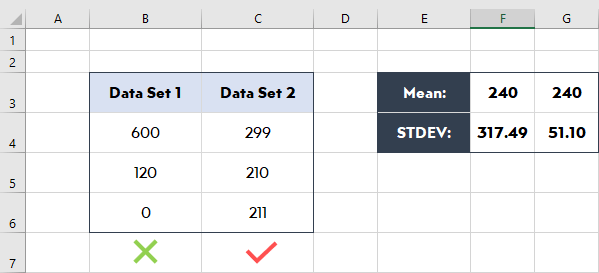
It is also not possible to compare data sets accurately without using standard deviations. Let’s say you have two data sets that have the same mean. One of them is 600,30,0 and 299,210,211. Both of them have the same average but the standard deviation is very different. While our first set is unreliable our second set is consistent.
In summary, the standard deviation is important because
- They are a key element of calculating the perimeters of error.
- It allows us the compare two different sets of data effectively.
- It shows us the risk by showing the range of data
Using standard deviation in real-life:
People use this statistic every day in their lives actually. It gives you a realistic opinion about the range in our data set so it is a popular formula. Some examples of standard deviation from our everyday life that might help you to understand the importance of this statistic:
-
When calculating the range to the average in a data set:
A class of students takes a physics test. The teacher finds out that the mean score on the test is 75%. Then the teacher decides to calculate the standard deviation to see if the grades were near 75%.
Standard deviations turn out to be very small and that means student grades were very close to 75%.

A class of students took a test in English Language and Literature. The teacher decides that the mean grade on the exam is 55%. She is concerned that this is very low, so she decides to calculate the standard deviation to see how many students scored close to the mean.
The teacher finds that the standard deviation is large. After closely checking all of the tests, the teacher is capable to conclude that numerous students with very low scores were the outliers that dragged down the mean of the entire class’s scores.
-
To find the outliers in a set of data:
A veterinarian wants to learn if the cats under his care are close in weight or not close in weight. He takes the average weight of all ten cats (the mean).

Then he calculates the variance, and then the standard deviation. His standard deviation is remarkably high. This implies that the cats are of many different weights, or that he has a few cats whose weights are outliers that are distorting the data.
-
While determining the reliability of the data:
A store researcher is examining the results of a recent customer survey. He wants to have some measure of the reliability of the answers taken in the survey in order to predict how a larger group of people might answer the same questions. A low standard deviation shows that the answers are very suitable for a larger group of people.
Another example would be a weather reporter when analyzing the high temperature calculated for a series of dates versus the actual high temperature recorded on each date. A low standard deviation would show a reliable weather forecast.
An employer wants to determine if the salaries in one department to see if it is fair for all employees, or if there is a big difference. She discovers the average of the salaries in that department and then calculates the variety, and then the standard deviation.
The employer finds that the standard deviation is slightly higher than he expected, so he studies the data further and finds that while most employees make similar salaries, three old employees who have been in the department for 15 years or more, notably longer than the others, are making far more due to their continuation with the company. Doing the analysis helped the employer to understand the range of salaries of the people in the department.
-
When determining a standard measurement
In production design, designers try to develop general sizing systems to determine the variations needed in the size of the product to produce sizes for everyone. Shirts for example. Or baby seats for cars. To do that designers use standard deviation so they can calculate how much difference they should have in the product line.
Standard Deviation In Sports
Why do we need statistics in sports? Just think it like you own a team:
- Ability to examine your team’s average of parameters in the main panel graphics in the graphs that compare the statistical average of other teams in the league.
- Determine the up / down trends by comparing the statistics of your own match with the other matches of your choice
- To be able to compare your own match data with match data of other teams in order to detect tactical changes.
- To be able to see the offensive, defensive, passing, and one-to-one parameters of your team’s success/failure very quickly side by side with the ratios of other teams.
Sports teams use standard deviation. For example, a team that may be consistently successful may have a low standard deviation, but a team that scores a lot of standard deviation might be high.
In recent years, the use of statistical analytics in sports has been on the rise. ESPN (sports streaming platform) has even given an entirely new segment of its webpage to sports analytics. New metrics to measure an athlete’s performance are seemingly being developed on a daily basis.
The Moneyball Theory
Have you seen the Hollywood movie Moneyball? The movie is about a baseball team (Oakland A’s) start using data to improve their games. It is basically the start of our sports world. Today, luring good players to the games is less important than collecting and process the data. Because data will show the managers were to improve this will improve the game and chance of winning the championship (assuming this is the ultimate goal).
This situation eventually created a theory called The Moneyball Theory. It gives answers to two simple things: Can the player hit? Can the player create runs? If the answer is yes then probably your team is in good hands.
This is the method Oakland A’s general manager Billy Beane used in 2002. He used the Moneyball Theory to select a team of underestimated players.

He and his team ended up winning 20 games in a row. Between 2000 to 2006, the Oakland A’s went on to average 95 wins, win four American League West medals, and made five playoff displays.
Just because someone thought determining the standard deviation and process it other than just settle with the mean or naked-eye observation today’s sports world changed entirely.
Free Download: League Schedule Maker Template
How to calculate standard deviation in Excel:
Now, since you have the information on what standard deviation is and how to use it you can start learning how to calculate it on Microsoft Excel.
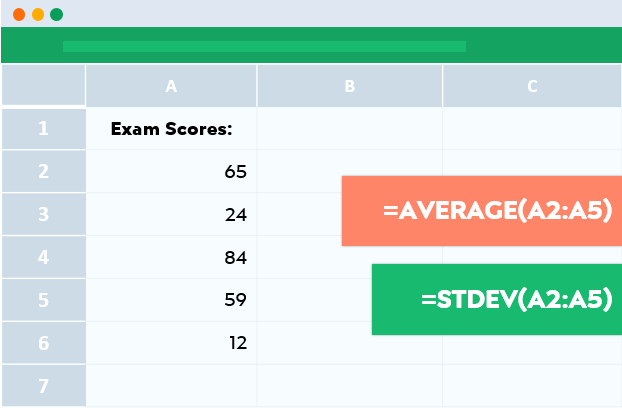
Excel is an office program that allows us to calculate the collected data. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications. But you can easily calculate the standard deviation with simple formulas.
Let’s begin.
There are eight standard deviation formulas in Excel. You can calculate the standard deviation of a sample or the entire data you have.
Sample calculations are common because sometimes it’s not possible to calculate entire data. And since you use sample calculations more often, let’s start with their formulas.
How to Use STDEV.S or STDEV?
To use STDEV.S you enter a really simple formula:
STDEV.S(number1, number2, number3…) or STDEV.S([number1], [number2], [number3],…
Number 1: This is the necessary argument in the formula. This is the very first element of the sample. You can use a single array, named range, or a reference to an array instead of using commas.
Number 2 and number 3: This is the optional argument. You can add arguments up to 254 arguments in Excel.
Let’s say you have exam scores dataset from A2 to A11:
You simply use the formula: =STDEV.S(A1:A11)
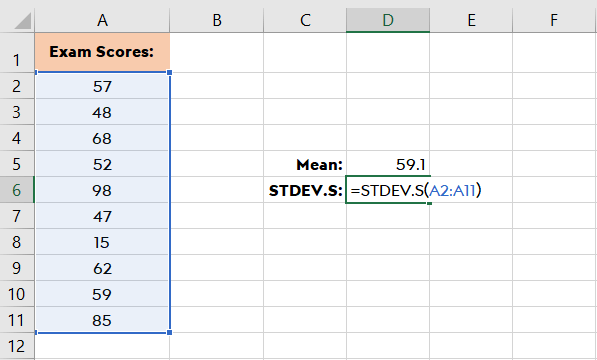
If you have a prior version of Excel you can use STDEV instead of STDEV.S. In the same scenario of STDEV.S, you use the formula: =STDEV(A2:A11)
If you want to learn more about Excel formulas check this Excel Practice worksheet.
How To Make Standard Deviation Calculations Manually?
Maybe you are not good with Excel formulas or you find them too complicated to use. You can always manually calculate your data. Let’s how to do that step by step.
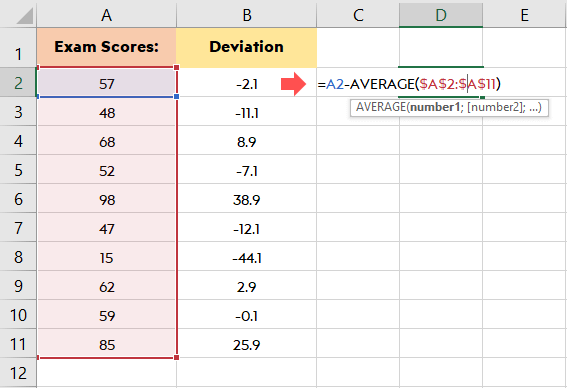
Let’s say you entered your data from A2 to A11:
After entering your data to your Excel sheet you should determine the deviation. It means value minus the mean. The formula for that is = A2 -AVERAGE($A$2:$A$11). The deviations values will be written in the B column starting with B2.
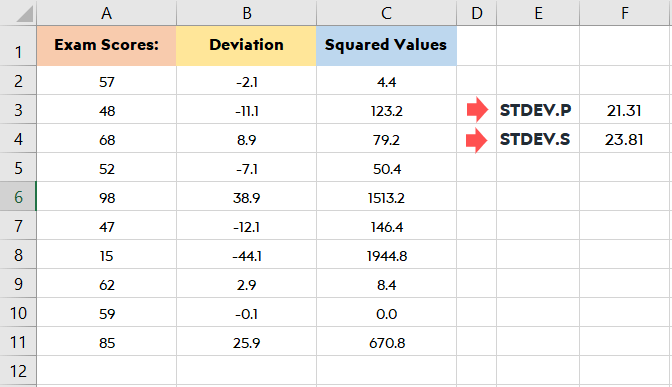
Once you calculate deviation you will need the squared value of your deviations. So if you had negatives values in the first calculations they will all turn to positive values. For that, you will use the formula: = (B2)^2. The squared values of the deviation will be written in column C starting with C2.

In E3 you can calculate the standard deviation for the population with this formula:
In E4 you can calculate standard deviation for a sample with:
That is it. You can easily calculate the standard deviation on Excel even when you have a large quantity of data. If you want to learn more about things you can do with Excel don’t forget to check our Complete List of Things You Can Do with Excel article.



